COMET method - a new quality in decision making
Currently existing multi-criteria decision-making (MCDM) methods yield results that may be questionable and unreliable. These methods very often ignore the issue of rank reversal paradox, which is a fundamental and essential challenge of MCDM methods. In response to this challenge, the Characteristic Objects Method (COMET) was developed. The classical COMET is entirely free of the rank reversal paradox.
COMET section - fundamental information about COMET algorithmCOMET software - COMET software with manual
References section - the most important papers about COMET
Contact section - contact to the author
COMET
This webpage presents preliminaries of the fuzzy sets theory and computational algorithm of the basic COMET method. In the Software section, COMET software and manual can be founded.
Fuzzy sets theory: preliminaries
Definition 1 The fuzzy set and the membership function
The characteristic function μA of a crisp set A ⊆ X assigns a value of either 0 or 1 to each member of X, as well as the crisp sets only allow a full membership μA(x)=1 or no membership at all μA(x)=0. This function can be generalized to a function μà so that the value assigned to the element of the universal set X falls within a specified range, i.e., μà : X → [0, 1]. The assigned value indicates the degree of membership of the element in the set à . The function μà is called a membership function and the set à ={(x,μà (x))}, where x ∈ X, defined by μà (x) for each x ∈ X, is called a fuzzy set.
Definition 2 The triangular fuzzy number (TFN)
A fuzzy set Ã, defined on the universal set of real numbers R, is told to be a triangular fuzzy number Ã(a,m,b) if its membership function has the following form:
and the following characteristics:
x1, x2 ∈ [a, b] ∧ x2 > x1 ⇒ μÃ(x2) > μÃ(x1)
x1, x2 ∈ [b, c] ∧ x2 > x1 ⇒ μÃ(x2) < μÃ(x1)
An example of triangular fuzzy number Ã(a,m,b) is presented:
Definition 3 The support of a TFN Ã
The support of a TFN à is defined as a crisp subset of the à set in which all elements have a non-zero membership value in the à set:
S(Ã) = {x: μ{Ã}(x) > 0} = [a, b] Definition 4 The core of a TFN Ã
The core of a TFN Ã is a singleton (one-element fuzzy set) with the membership value equal to 1:
C(Ã) = {x: μÃ(x) = 1} = m Definition 5 The fuzzy rule
The single fuzzy rule can be based on the Modus Ponens tautology. The reasoning process uses the IF-THEN, OR and AND logical connectives.
Definition 6 The rule base
The rule base consists of logical rules determining the causal relationships existing in the system between the input and output fuzzy sets.
Definition 7 The T-norm operator: product
The T-norm operator is a T function modeling the AND intersection operation of two or more fuzzy numbers, e.g. Ã and &Btilde;$. In the basic approach, only the ordinary product of real numbers is used as the T-norm operator:
μA(x) AND μB(y) = μA(x) · μB(y)
The Characteristic Objects Method
Step 1. Definition of the space of the problem
The expert determines the dimensionality of the problem by selecting r criteria, C1, C2, ..., Cr. Then, a set of fuzzy numbers is selected for each criterion Ci, e.g. {Ci1, Ci2, ..., Cici}:where c1,c2, ...,cr are the ordinals of the fuzzy numbers for all criteria.
Step 2. Generation of the characteristic objects
The characteristic objects CO are obtained with the usage of the Cartesian product of the fuzzy numbers' cores of all the criteria:As a result, an ordered set of all $CO$ is obtained: where t is the count of COs and is equal to:
Step 3. Evaluation of the characteristic objects
The expert determines the Matrix of Expert Judgment )MEJ) by comparing the COs pairwise. The matrix is presented below:where αij is the result of comparing COi and COj by the expert. The function fexp denotes the mental judgment function of the expert. It depends solely on the knowledge of the expert. The expert's preferences can be presented as: After the MEJ matrix is prepared, a vertical vector of the Summed Judgments SJ is obtained as follows: Eventually, the values of preference are approximated for each characteristic object. As a result, a vertical vector P is obtained, where the i-th row contains the approximate value of preference for COi.
Step 4. The rule base
Each characteristic object and its value of preference is converted to a fuzzy rule as follows:In this way, a complete fuzzy rule base is obtained.
Step 5. Inference and the final ranking
Each alternative is presented as a set of crisp numbers, e.g.:Ai={a1i, a2i, ..., ari} This set corresponds to the criteria C1, C2, ..., Cr. Mamdani's fuzzy inference method is used to compute the preference of the i-th alternative. The rule base guarantees that the obtained results are unequivocal. The COMET is completely free of rank reversal.
Software
Projects
NCN OPUS
A new method for determining the significance level of decision criteria based on characteristic objects
The project aims to develop a new method for determining the significance levels (weights) of decision criteria using
characteristic objects. Unlike traditional approaches, the proposed solution considers both global and local weights,
accounting for how each criterion's importance changes depending on context and the current “saturation” level of the
attribute in question. This makes the evaluation of alternatives in multi-criteria decision-making processes—such as
official tenders or product rankings—more accurate and better suited to real-world needs.
The project is supported by the National Science Centre, the agreement no. UMO-2021/41/B/HS4/01296
List of publications:
-
Wątróbski, J., Bączkiewicz, A., Król, R., & Sałabun, W. (2022).
Green electricity generation assessment using the CODAS-COMET method.
Ecological Indicators, 143, 1-32.
-
Devi, P., Kizielewicz, B., Guleria, A., Shekhovtsov, A., Wątróbski, J., Królikowski, T.,
Więckowski, J., & Sałabun, W. (2022). Decision Support in Selecting a Reliable Strategy
for Sustainable Urban Transport Based on Laplacian Energy of T-Spherical Fuzzy Graphs.
Energies, 15(14), 1-20, [art. no. 4970].
-
Thakur, P., Kizielewicz, B., Gandotra, N., Shekhovtsov, A., Saini, N., & Sałabun, W. (2022).
The Group Decision-Making Using Pythagorean Fuzzy Entropy and the Complex Proportional Assessment.
Sensors, 22(13), 1-17, [art. no. 4879].
-
Sultan, A., Sałabun, W., Faizi, S., Ismail, M., & Shekhovtsov, A. (2022).
Making Group Decisions within the Framework of a Probabilistic Hesitant Fuzzy Linear Regression Model.
Sensors, 22(15), 1-17, [art. no. 5736].
-
Shekhovtsov, A., Kizielewicz, B., & Sałabun, W. (2023).
Advancing individual decision-making: An extension of the characteristic objects method using expected solution
point.
Information Sciences, 647, 1-24.
-
Więckowski, J., Sałabun, W., Kizielewicz, B., Bączkiewicz, A., Shekhovtsov, A., Paradowski, B., & Wątróbski, J.
(2023).
Recent advances in multi-criteria decision analysis: A comprehensive review of applications and trends.
International Journal of Knowledge-based and Intelligent Engineering Systems, 27, 367-393.
-
Kaczyńska, A., Sulikowski, P., Wątróbski, J., & Sałabun, W. (2023).
Enhancing Sustainable Assessment of Electric Vehicles: A Comparative Study of the TOPSIS Technique
with Interval Numbers for Uncertainty Management.
Energies, 16(18), 1-17.
-
Więckowski, J., Kizielewicz, B., & Sałabun, W. (2023).
Handling decision-making in Intuitionistic Fuzzy environment: PyIFDM package.
SoftwareX, 22, 1-8.
-
Więckowski, J., Kizielewicz, B., Shekhovtsov, A., & Sałabun, W. (2023).
How Do the Criteria Affect Sustainable Supplier Evaluation? - A Case Study Using Multi-Criteria Decision
Analysis Methods
in a Fuzzy Environment.
Journal of Engineering Management and Systems Engineering, 2(1), 37-52.
-
Kizielewicz, B., Shekhovtsov, A., & Sałabun, W. (2023).
pymcdm—The universal library for solving multi-criteria decision-making problems.
SoftwareX, 22, 1-8.
-
Więckowski, J., & Sałabun, W. (2023).
Sensitivity analysis approaches in multi-criteria decision analysis: A systematic review.
Applied Soft Computing, 148, 1-19.
-
Shekhovtsov, A., Kizielewicz, B., & Sałabun, W. (2023).
Version [1.1] - [pymcdm – The universal library for solving multi-criteria decision-making problems].
SoftwareX, 24, 1-5.
-
Więckowski, J., & Sałabun, W. (2024).
Version [1.1]- [pyFDM: A python library for uncertainty decision analysis methods].
SoftwareX, 25, 1-4.
-
Więckowski, J., Kizielewicz, B., Chmielarz, W., & Sałabun, W. (2024).
Version [1.1]- [Handling decision-making in intuitionistic fuzzy environment: PyIFDM package].
SoftwareX, 25, 1-5.
-
Więckowski, J., & Sałabun, W. (2024).
MakeDecision: Online system for the graphical design of decision-making models in crisp and fuzzy environments.
SoftwareX, 26, 1-7.
-
Więckowski, J., & Sałabun, W. (2024).
A new sensitivity analysis method for decision-making with multiple parameters modification.
Information Sciences, 678, 1-19.
-
Paradowski, B., Więckowski, J., & Sałabun, W. (2024).
PySensMCDA: A novel tool for sensitivity analysis in multi-criteria problems.
SoftwareX, 27, 1-8.
-
Kizielewicz, B., Shekhovtsov, A., Więckowski, J., Wątróbski, J., & Sałabun, W. (2102).
The Compromise-COMET Method for Identifying an Adaptive Multi-Criteria Decision Model.
IEEE Access, 12, 157083-157106.
-
Kizielewicz, B., Paradowski, B., Więckowski, J., & Sałabun, W. (2022).
Towards the identification of MARCOS models based on intuitionistic fuzzy score functions.
Annals of Computer Science and Information Systems (Proceedings of the 17th Conference on Computer
Science and
Intelligence Systems, 4-7.09.2022), 789-798.
-
Kizielewicz, B., Shekhovtsov, A., & Sałabun, W. (2022).
A novel iterative approach to determining compromise rankings.
Annals of Computer Science and Information Systems (Proceedings of the 17th Conference on Computer
Science and
Intelligence Systems, 4-7.09.2022), 783-787.
-
Sałabun, W., & Shekhovtsov, A. (2023).
An Innovative Drastic Metric for Ranking Similarity in Decision-Making Problems.
Proceedings of the 18th Conference on Computer Science and Intelligence Systems (17-20.09.2023), 731-738.
NCN Preludium
A new method using reference objects to support decision-making process in multi-criteria problems under uncertainty
The objective of the proposed research is to develop a new method using reference objects to support decision-making in multi-criteria problems under uncertainty.
The motivation for the proposed research is the fact that in many areas of science, including, behavioral economics, sustainable development or the management, we are dealing more and more with multi-criteria problems whose solution is sought in the conditions of uncertainty. It means that important decision problems involving mostly a lot of contradictory criteria are also considered using imprecise or uncertain data and information.
The project is supported by the National Science Centre, the agreement no. UMO-2016/23/N/HS4/0193
List of publications:
- Multicriteria Selection of Online Advertising Content for the Habituation Effect Reduction (in press)
- Sałabun, W., Karczmarczyk, A., Wątróbski, J., & Jankowski, J. (2018, November). Handling Data Uncertainty in Decision Making with COMET. In 2018 IEEE Symposium Series on Computational Intelligence (SSCI) (pp. 1478-1484). IEEE.
- Sałabun, W., Karczmarczyk, A., & Wątróbski, J. (2018, November). Decision-Making using the Hesitant Fuzzy Sets COMET Method: An Empirical Study of the Electric City Buses Selection. In 2018 IEEE Symposium Series on Computational Intelligence (SSCI) (pp. 1485-1492). IEEE.
- Sałabun, W., & Karczmarczyk, A. (2018). Using the comet method in the sustainable city transport problem: an empirical study of the electric powered cars. Procedia computer science, 126, 2248-2260.
- Faizi, S., Sałabun, W., Rashid, T., Wątróbski, J., & Zafar, S. (2017). Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry, 9(8), 136.
- Wątróbski, J., Sałabun, W., Karczmarczyk, A., & Wolski, W. (2017, September). Sustainable decision-making using the COMET method: An empirical study of the ammonium nitrate transport management. In 2017 Federated Conference on Computer Science and Information Systems (FedCSIS) (pp. 949-958). IEEE.
- Bashir, Z., Wątróbski, J., Rashid, T., Sałabun, W., & Ali, J. (2017). Intuitionistic-fuzzy goals in zero-sum multi criteria matrix games. Symmetry, 9(8), 158.
NCN Preludium
A new method using reference objects to support decision-making process in multi-criteria problems under uncertainty
The objective of the proposed research is to develop a new method using reference objects to support decision-making in multi-criteria problems under uncertainty. The motivation for the proposed research is the fact that in many areas of science, including, behavioral economics, sustainable development or the management, we are dealing more and more with multi-criteria problems whose solution is sought in the conditions of uncertainty. It means that important decision problems involving mostly a lot of contradictory criteria are also considered using imprecise or uncertain data and information. The project is supported by the National Science Centre, the agreement no. UMO-2016/23/N/HS4/0193List of publications:
- Multicriteria Selection of Online Advertising Content for the Habituation Effect Reduction (in press)
- Sałabun, W., Karczmarczyk, A., Wątróbski, J., & Jankowski, J. (2018, November). Handling Data Uncertainty in Decision Making with COMET. In 2018 IEEE Symposium Series on Computational Intelligence (SSCI) (pp. 1478-1484). IEEE.
- Sałabun, W., Karczmarczyk, A., & Wątróbski, J. (2018, November). Decision-Making using the Hesitant Fuzzy Sets COMET Method: An Empirical Study of the Electric City Buses Selection. In 2018 IEEE Symposium Series on Computational Intelligence (SSCI) (pp. 1485-1492). IEEE.
- Sałabun, W., & Karczmarczyk, A. (2018). Using the comet method in the sustainable city transport problem: an empirical study of the electric powered cars. Procedia computer science, 126, 2248-2260.
- Faizi, S., Sałabun, W., Rashid, T., Wątróbski, J., & Zafar, S. (2017). Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry, 9(8), 136.
- Wątróbski, J., Sałabun, W., Karczmarczyk, A., & Wolski, W. (2017, September). Sustainable decision-making using the COMET method: An empirical study of the ammonium nitrate transport management. In 2017 Federated Conference on Computer Science and Information Systems (FedCSIS) (pp. 949-958). IEEE.
- Bashir, Z., Wątróbski, J., Rashid, T., Sałabun, W., & Ali, J. (2017). Intuitionistic-fuzzy goals in zero-sum multi criteria matrix games. Symmetry, 9(8), 158.
References
Journals
- Sałabun, W., & Karczmarczyk, A. (2018). Using the comet method in the sustainable city transport problem: an empirical study of the electric powered cars. Procedia computer science, 126, 2248-2260.
- Faizi, S.; Sałabun, W.; Rashid, T.; Wątróbski, J.; Zafar, S. Group Decision-Making for Hesitant Fuzzy Sets Based on Characteristic Objects Method. Symmetry 2017, 9, 136.
- Faizi, S., Rashid, T., Sałabun, W., Zafar, S., Wątróbski, J. (2017). Decision Making with Uncertainty Using Hesitant Fuzzy Sets. International Journal of Fuzzy Systems, 1-11.
- Sałabun, W., Piegat, A. (2016). Comparative analysis of MCDM methods for the assessment of mortality in patients with acute coronary syndrome. Artificial Intelligence Review, 1-15.
- Sałabun, W., Napierała, M., Bykowski, J. (2015). The Identification of Multi-Criteria Model of the Signicficance of Drainage Pumping Stations in Poland. Acta Scientiarum Polonorum. Formatio Circumiectus, 14(3), 147-163.
- Sałabun, W. (2015). Assessing the 10-year risk of hard arteriosclerotic cardiovascular disease events using the characteristic objects method. Studies & Proceedings Polish Association for Knowledge Management, 77, 65-76.
- Sałabun, W. (2015). Fuzzy Multi-Criteria Decision-Making Method: the Modular Approach in the Characteristic Objects Method. Studies & Proceedings of Polish Association for Knowledge Management, 77, 54-64.
- Sałabun, W. (2015). The Characteristic Objects Method: A New Distance‐based Approach to Multicriteria Decision‐making Problems. Journal of Multi-Criteria Decision Analysis, 22(1-2), 37-50.
- Sałabun, W. (2014). Reduction in the number of comparisons required to create matrix of expert judgment in the comet method. Management and Production Engineering Review, 5(3), 62-69.
- Sałabun, W. (2014). Application of the fuzzy multi-criteria decision-making method to identify nonlinear decision models. Interantional Journal of Computer Applications, 89(15), 1-6.
- Piegat, A., Sałabun, W. (2014). Identification of a multicriteria decision-making model using the characteristic objects method. Applied Computational Intelligence and Soft Computing, 2014, 14.
- Piegat, A., Sałabun, W. (2012). Nonlinearity of human multi-criteria in decision-making. Journal of Theoretical and Applied Computer Science, 6(3), 36-49.
- Sałabun, W. (2012). The use of fuzzy logic to evaluate the nonlinearity of human multi-criteria used in decision making. Przegląd Elektrotechniczny, 88(10b), 235-238.
Chapters
- Sałabun, W., Karczmarczyk, A., Wątróbski, J., & Jankowski, J. (2018, November). Handling Data Uncertainty in Decision Making with COMET. In 2018 IEEE Symposium Series on Computational Intelligence (SSCI) (pp. 1478-1484). IEEE.
- Sałabun, W., Karczmarczyk, A., & Wątróbski, J. (2018, November). Decision-Making using the Hesitant Fuzzy Sets COMET Method: An Empirical Study of the Electric City Buses Selection. In 2018 IEEE Symposium Series on Computational Intelligence (SSCI) (pp. 1485-1492). IEEE.
- Wątróbski, J., Sałabun, W., Karczmarczyk, A., Wolski, W. (2017). Sustainable Decision-Making using the COMET Method: An Empirical Study of the Ammonium Nitrate Transport Management. In press.
- Jankowski, J., Sałabun, W., Wątróbski, J. (2017). Identification of a multi-criteria assessment model of relation between editorial and commercial content in web systems. In Multimedia and Network Information Systems (pp. 295-305). Springer International Publishing.
- Sałabun, W., Wątróbski, J., & Piegat, A. (2016, June). Identification of a Multi-criteria Model of Location Assessment for Renewable Energy Sources. In International Conference on Artificial Intelligence and Soft Computing (pp. 321-332). Springer, Cham.
- Sałabun, W., Ziemba, P., Wątróbski, J. (2016). The Rank Reversals Paradox in Management Decisions: The Comparison of the AHP and COMET Methods. In Intelligent Decision Technologies 2016 (pp. 181-191). Springer International Publishing.
- Watróbski, J., Sałabun, W. (2016). The characteristic objects method: a new intelligent decision support tool for sustainable manufacturing. In Sustainable Design and Manufacturing 2016 (pp. 349-359). Springer International Publishing.
- Sałabun, W., Ziemba, P. (2016). Application of the Characteristic Objects Method in Supply Chain Management and Logistics. In Recent Developments in Intelligent Information and Database Systems (pp. 445-453). Springer International Publishing.
- Piegat, A., Sałabun, W. (2015, June). Comparative analysis of MCDM methods for assessing the severity of chronic liver disease. In International Conference on Artificial Intelligence and Soft Computing (pp. 228-238). Springer, Cham.
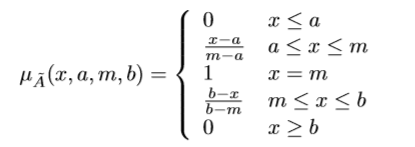


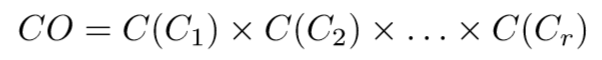
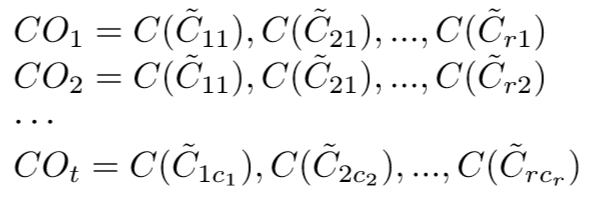
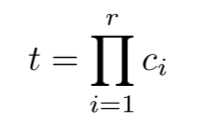

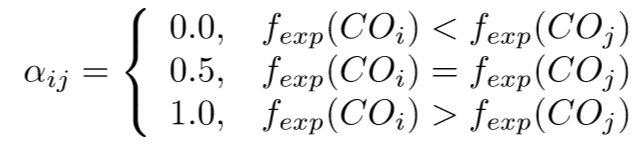
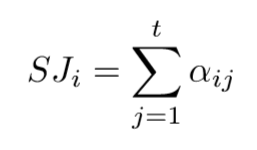
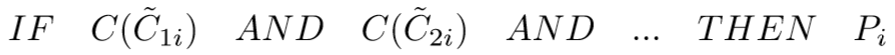
 ORCID
ORCID Scopus
Scopus Google Scholar
Google Scholar